Soluzioni
Subito subito,
Quesito 1, la zona colorata ...
Per la classe seconda risolvono: Gian Franco, Alessia, Elisa, Antonella, Miriam.
Alessia, sua la figura sotto, così spiega (riporto anche i colori-carattere da lei utilizzati su geogebra):
Per prima cosa calcolo quanti triangoli “colorati” ci sono nella prima riga in basso (5) poi moltiplico per quante volte si ripete la stessa riga [altezza del rettangolo viola (4)]. 5*4=20 cm²
Poi immagino che, nella parte superiore, un parallelogramma, formato da 4 triangolini, sia “tagliato” in 2 parti congruenti dalla diagonale.
Quindi l'area del parallelogramma viene divisa in due:
4/2 = 2 cm² = area della metà del parallelogramma.
Infine aggiungo 0,5 cm², che è l'area del piccolo triangolo blu, alla metà del parallelogramma.
Totale:
20 cm²+ 2,5 cm² = 22,5 cm²= area della parte colorata
Gian Franco, Miriam, Antonella e Elisa, ma quest’ultima solo parzialmente, riportano più o meno la stessa spiegazione. Quella che segue è di Gian Franco:
Dopo aver fatto la somma dei triangoli interi e le metà che si trovavano ai lati ho ottenuto una somma di 20,5 cm². Mi rimanevano ora 4 pezzi di triangoli che, ho notato, andavano bene a coppie per riempire due triangoli. Ma siccome non ero sicuro per poterlo dimostrare, ho preso in considerazione il parallelogramma formato da quattro triangoli interi. Poiché la diagonale del parallelogramma lo divide in due parti congruenti, ho potuto confermare che la parte colorata corrispondeva alla metà del parallelogramma cioè due triangoli.
Area totale = 22,5 cm².
Gian Franco in verità, da me invitato ad una soluzione alternativa, sollecitato ad osservare bene le dimensioni del triangolo rettangolo individuato sopra la porzione rettangolare, riesce a “vedere” che: la base del triangolo rettangolo è uguale a 2,5 volte quella del triangolino e la sua altezza è la stessa altezza del triangolino, maa: non riesce a concludere che:
se un triangolo ha la base 2,5 volte quella di un altro triangolo e la stessa altezza, allora la sua area è 2,5 volte maggiore.
Essendo dunque l’area del triangolino di 1 cm², quella del triangolo rettangolo è di 2,5 cm²
... Eppure qualcosa avevamo già visto sulla variazione delle aree al variare di una dimensione. Sì, non abbiamo ancora troppo insistito, ma ho l’impressione che a impedire la conclusione da parte di Gian Franco sia stato quel ...decimale! 2,5 acci! Se la base fosse stata semplicemente “doppia”, probabilmente sarebbe scappato un: “allora l’area è doppia”. Chissà ...
Per la classe terza “partecipano”: Bachisio, Gabriele G., Pietro S., Marco.
Bachisio realizza la costruzione su geogebra, anche in maniera rapida: ha usato una macro, bravo!
E spiega:
-All’interno dell’area colorata ci sono 16 triangoli equilateri interi, quindi abbiamo già 16 cm² .
-I pezzi di triangolo ai lati della figura equivalgono alla metà di un triangolo, perché se guardiamo con attenzione, ci accorgiamo che ci sono dei rombi tagliati in 4 parti (1/4 di rombo= ½ di triangolo). Da tutti questi mezzi triangoli ottengo 4,5 cm².
-Gli ultimi 4 pezzi di triangolo equivalgono a due triangoli, basta guardare il parallelogramma tagliato a metà dalla sua diagonale (siccome la metà di 4 è 2…). Quindi otteniamo altri 2 cm².
QUINDI: 16 cm² + 4,5 cm² + 2 cm² = 22,5 cm² = A_colorata.
(Ho invitato anche Bachisio, con più strumenti dei compagni di seconda, alla soluzione alternativa, ma: nulla di fatto).
Gabriele dice (a tratti molto didascalico):
Mi sono accorto che l’area della parte rettangolare è di 20 cm², essendo formata da 8 mezzi triangolini (di area 0,5 cm²) e 16 triangolini interi (di area 1 cm²).
Per completare la parte colorata rimaneva un triangolo rettangolo, che se “ricomposto” è formato da 2 triangolini e mezzo.
Quindi facendo due calcoli viene 1 cm² * 2 triangolini + 0,5 cm² *1 mezzo triangolino = 2 + 0,5 = 2,5 cm², che sommati all’area del rettangolo viene 20 cm² + 2,5 cm² = 22,5 cm² .
E invia la figura seguente:
Spiega così la sua ricomposizione. Senza parole, nient’affatto didascalico stavolta, ad occhio, insomma. E io, nient’affatto soddisfatta!
Pietro S. e Marco invece, variano soluzione (bene!):
L'area della zona colorata è 22,5 cm²: per saperlo ho diviso la figura in due poligoni, un rettangolo e un triangolo rettangolo. Ho controllato quanti triangoli ci sono in ogni riga del rettangolo e sono 5 perché 4 interi e 2 metà, ci sono 4 righe e quindi 5*4=20 cm². Per trovare l'area del triangolo rettangolo ho diviso una riga (del rettangolo) in due perché esso ha stessa base e stessa altezza di una riga del rettangolo.
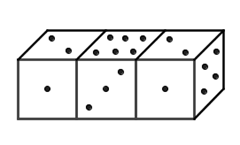
Quesito 2, i dadi...
Solutori seconda: Gian Franco, Alessia e Antonella. Eh... Miriam e Elisa hanno lavorato meno, stavolta!
I tre spiegano tutti allo stesso modo, copio la soluzione-Gian Franco, completa seppure a tratti un po’ contorta!
Le somme sono: 5 (a destra) e 9 (a sinistra).
Sono partito dal dado più a destra, perché era il più completo: i punti della faccia nascosta sono 3. Poi sono passato al dado centrale, ma ai lati ci poteva essere o il 2 o il 5. Quindi dopo averlo osservato per bene ho immaginato di ruotarlo in modo da fargli assumere la stessa posizione del dado a destra. L'ho “ruotato” prima a sinistra e poi verso l'alto per ottenere le stesse facce davanti e dietro e infine ho messo i numeri uguali a quelli dell'altro dado cioè il 2 sopra e il 5 sotto. Poi l'ho riportato nella posizione di prima e avevo il 2 a destra e il 5 a sinistra.
Sono passato al dado di sinistra e ho notato che era nella stessa posizione di quello di destra quindi non mi restava che mettere i numeri nascosti nelle stesse posizioni ottenendo al lato destro il 4. Il dado centrale combacia con questa faccia con i 5 punti.
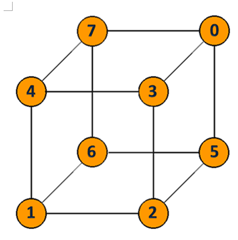
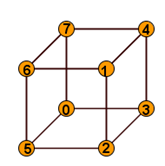
Infine ho preso una scatolina e ci ho scritto i numeri nelle stesse posizioni di quelle del dado di destra, poi l'ho ruotato nella posizione di quello centrale cioè il 3 davanti, il 6 sopra, l' 1 sotto e il 4 dietro e ho notato che le posizioni del 2 e del 5 corrispondevano a quelle che io avevo già immaginato all'inizio.
Solutori terza: Bachisio, Pietro S. e Marco. Pietro P., sbrigativo, mi scrive i punti che stanno sulle facce che combaciano, verosimilmente fatica troppo ad eseguirne la somma! Gabriele G. NON risolve correttamente.
Le risposte in sintesi:
-La faccia interna del dado a destra è di 3 perché 7-4 (la faccia opposta) = 3 [*I punti che stanno...* così anche per ciò che segue]
- Le due facce interne del dado centrale sono 2 e 5, perché 3 e 6 sono visibili, l’1 si trova sotto (6+1=7) e il 4 che si trova dietro(3+4=7).
-La faccia interna del cubo a sinistra è 4 perché il dado si trova nella stessa posizione di quello a destra.
- Quindi la somma dei punti delle facce che combaciano è: 3+2+5+4=14.
Ho concluso. Anzi, conclusione con rima:
Solite lodi a chi ha lavorato,
che come sempre ha guadagnato!
Ecco, rideteci su... Ma mica troppo, eh.
Prox appuntamento: sarà il nuovo Sarà mica... del prof Davide. Sì, no? Noi teniamoci pronti!