Ancora una volta,
finalmente, le soluzioni.
Impegni, intoppi, ..., a volte impediscono la puntualità, il rispetto delle scadenze.
Ecco dunque le soluzioni.
Quesito n° 1, quello numerico.
I solutori. Per la classe seconda: Alessia, Miriam, Erika, Gian Franco, Giuseppe P., Elisa, Cristiana, Arianna.
Nelle risposte ha prevalso il ragionamento che chiamerei un po’ per tentativi, e seguendo le operazioni inverse, seppure con qualche valida considerazione. Riporto qualche e mail.
Elisa scrive:
secondo me Luisa ha pensato al numero 12, poi Marco l'ha moltiplicato x 6, Sonia ha aggiunto 6 e infine Dino ha tolto 5.
12x6=72; 72+6=78; 78-5=73
Ho ragionato così: dovevo trovare un multiplo, o di 6 o di 5 che fosse più vicino a 73, perché 73 non è multiplo né di 5 né di 6, quindi Sonia e Dino non possono aggiungere e togliere lo stesso numero. Allora ho pensato il 12 che moltiplicato per 6 da 72, bhe, da qui era facile proseguire, avrei aggiunto 6 e poi tolto 5 ottenendo così il 73.
Gian Franco spiega diversamente:
Ho risolto il quesito inizialmente generalizzando le operazioni fatte dalle persone del problema:
a x 6 o 5=b; b + 6 o 5=c; c - 6 o 5=73
ho fatto poi l'inverso dello schema:
73 + 6 o 5=c; c - 6 o 5=b; b : 6 o 5=a
a questo punto ho provato se il numero esatto era il 5 o il 6. Alla fine ho ottenuto questo risultato:
73 + 5=78; 78 - 6=72; 72 : 6=12
la prova ancora inversa mi dimostra che il numero pensato è il 12.
Solutori per la classe terza: Pierluigi, Gabriele G., Bachisio, Manuel, Pietro S.
Stavolta dalla terza arrivano risposte più soddisfacenti Anche qui qualche mail
Manuel dice:
se Sonia ha addizionato lo stesso numero sottratto da Dino, il 73 dovrebbe essere il prodotto ottenuto da Marco.
Il 73 è un numero primo, quindi è impossibile che Marco lo abbia ottenuto perché non è multiplo né di 5 né di 6 quindi seguono 2 strade:
1) Sonia ha addizionato 5 e Dino ha sottratto 6, Dino ottiene così il prodotto di Marco -1, quindi per sapere quanto ha ottenuto Marco bisogna fare il risultato di Dino+1. Si ottiene così 74 che non è divisibile né per 5 né per 6, non può essere quindi il risultato ottenuto da Marco.
2) Sonia ha addizionato 6 e Dino ha sottratto 5, Dino ottiene così il prodotto ottenuto da Marco +1, quindi per sapere quanto ha ottenuto Marco bisogna fare il risultato di Dino -1. Si ottiene così 72 che non è divisibile per 5, ma per 6. Il numero pensato da Luisa è quindi 12 (72/6=12).
Pietro S. (qui sono dovuta intervenire sulla forma, ma il ragionamento era tanto bello ):
il numero è 12: il prodotto ottenuto da Marco doveva essere un numero maggiore o minore di 73 (che non è multiplo né di 5 né di 6) ma solo di una unità. Non poteva essere 74 perché non è multiplo né di 5 né di 6. E’ invece 72 perché 12 * 6 = 72. A quel punto so che Sonia addiziona 6 e Dino toglie 5, così ottiene 73.
Bachisio (c’è Bachisio, stavolta ha consegnato su chiavetta USB!):
Avendo come dato certo il risultato (73), sono partito da qui:
tenendo conto che gli ultimi due passaggi mi davano la possibilità di sottrarre/aggiungere un’unità al 73, o lasciarlo inalterato, ho dedotto che il numero ottenuto da Marco, poteva andare dal 72 al 74.
Dopo aver diviso i tre numeri (72,73,74) sia per il 6 che per il 5, [ah, e hai pure eseguito le divisioni??? Prevederne la non divisibilità, no?] ho ottenuto un solo quoziente intero, 72/6=12.
Quindi Luisa ha pensato al 12. Marco lo ha moltiplicato per 6. Sonia ha aggiunto 6. Dino ha sottratto 5: 12*6+6-5=73
Quesito n° 2, quello geometrico
Solutori seconda: Alessia, Erika, Gian Franco, Elisa, Giuseppe P., Antonella
Sintesi delle risposte:
la linea spezzata misura 72 cm.
Spiegazione:
Dopo aver osservato attentamente la figura ho notato che la linea spezzata era formata da 3 lati di ciascun quadrato (il quarto lato si trova nel segmento AP). Poi siccome il segmento AP è formato dalla somma delle misure del lato di ciascun quadrato, per trovare la lunghezza della linea spezzata devo moltiplicare la misura del segmento AP, 24 cm, per 3, ottenendo 72 cm.
Per la terza: Pierluigi, Gabriele G., Bachisio, Manuel, Pietro S
Risultati corretti, più o meno equivalenti le spiegazioni:
La spezzata ABC...OP è lunga 72 cm (lunghezza AP *3 ). Infatti la spezzata è composta da tre lati di ciascun quadrato.
Essendo in possesso della somma dei lati di tutti i quadrati (AP=24), se moltiplico tale somma per 3, ottengo la misura della somma delle lunghezze dei 3 lati (per ogni quadrato) che forma la spezzata in questione.
Un altro ragionamento (è di Bachisio):
Sul segmento AP sono indicati tanti segmentini, su ognuno dei quali è costruito un quadrato.
La somma dei perimetri dei vari quadrati è uguale al perimetro dell’ipotetico quadrato costruito sul lato AP di cm 24. Quindi ho fatto 24*4=96. Il quesito mi chiede la lunghezza della linea spezzata (ABC…OP) che corrisponde alla somma di tre lati dell’ipotetico quadrato, quindi ho sottratto da 96 il 24, ottenendo così la lunghezza della spezzata ossia 72 cm.
Ok, mi pare di aver detto tutto. Come sempre, se dimentico qualcosa o qualcuno, mi si faccia notare.
Non scordo invece il BRAVO a chi ha lavorato!
Tenetevi pronti tutti per i nuovi quesiti del prof Davide. Siete fortunati: avrete, immagino, tutte le vacanze natalizie a disposizione....
Ora io vado a leggere le risposte dei suoi ragazzi. E voi, che fate?
Home page * GeoGebra * Excel * Matematica nella Storia. I Grandi Matematici * Matematica ricreativa * Libri * Le Curve Celebri * Immagini per la Matematica * Tutoriali * Le Formule più belle * Matematica e ... *
Altri modi per visualizzare il blog
INFORMATIVA SULLA PRIVACY E SUI COOKIE
*MATERIALE DIDATTICO *Risorse didattiche e SCUOLA *BLOG DIDATTICI e colleghicheleggo *Risorse EXCEL - OFFICE *Info CREARE e ARRICCHIRE IL PROPRIO BLOG *Altro Blogroll *Condivisioni *Visualizzazione formule matematiche
giovedì 18 dicembre 2014
Soluzioni Due a settimana..._9
Etichette: Due a settimana, matematica ricreativa
sabato 29 novembre 2014
Due a settimana..._9
Tutti pronti per i nuovi giochi?
Ecco pronti i giochi!
Quesito n° 1, numerico. Leggete con attenzione!
Luisa ha pensato un numero intero. Marco lo ha moltiplicato per 5 o per 6, ma non sappiamo per quale dei due. Sonia ha sommato al risultato ottenuto da Marco uno tra i due numeri 5 o 6, ma non sappiamo quale. Dino ha sottratto al risultato ottenuto da Sonia uno tra i due numeri 5 o 6, ma non sappiamo quale.
Alla fine Dino ci ha comunicato il risultato da lui ottenuto: 73. Che numero ha pensato Luisa?
Quesito n°2, geometrico
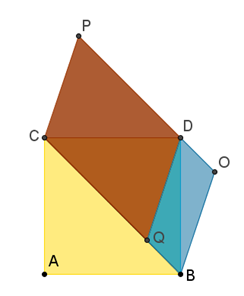
I quadrati che vedete in figura sono stati formati intersecando il segmento AP, lungo 24 cm, con la linea spezzata ABC...OP. Quanti centimetri è lunga la spezzata ABC...OP?
[benjamin '07 - Kangourou Italia]
Ovviamente anche questo va letto con attenzione e osservata la figura con altrettanta attenzione.
E’ il caso di ricordare che dovete motivare, spiegare le risposte? No, non è il caso
Buoni giochi (e buon impegno) a tutti!
Per la consegna avete tempo fino a domenica 14 dicembre ‘14
Etichette: Due a settimana, matematica ricreativa
venerdì 28 novembre 2014
Sarà mica matematica 31, le nostre soluzioni
Finalmente, eccole!
Le soluzioni del
Quesito n° 1, ah belli i quadrati ocigam, plurale icigam! Belli ma... danno un bel da fare le correzioni
Voi ragazzi avete provato a fare una ricerca su questi speciali quadrati? Certo che no, vi siete arresi allo scherzo del prof Davide, da me poi sorretto.
Se invece lo aveste fatto avreste trovato che tali quadrati sono chiamati quadrati eteromagici.
*Casi molto particolari di quadrati eteromagici sono i quadrati antimagici. Per questi ultimi le somme di righe, colonne e diagonali forniscono numeri interi consecutivi.
Veniamo alle soluzioni.
Molti di voi hanno usato il foglio di calcolo. Bene, mi avete dato una bella mano per il controllo, ma in compenso (tranne poche eccezioni) mi avete fatto faticare abbastanza per la formattazione che permettesse il ritaglio dell’immagine. Osservate bene le immagini e, soprattutto, pena rifiuto lavori futuri, seguite i suggerimenti dati per l’uso del foglio di calcolo! Le celle sono fatte per contenere dei dati, non servono troppi spazi bianchi (tante righe, colonne vuote). Né servono caratteri cubitali, né tante scritte per esteso... ecc.
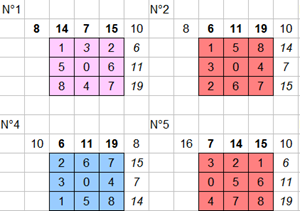
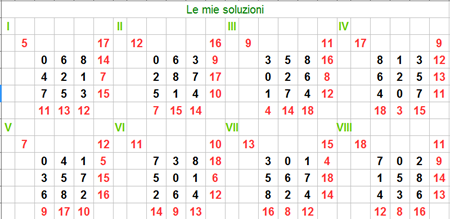
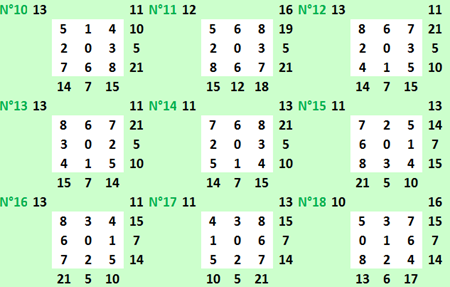
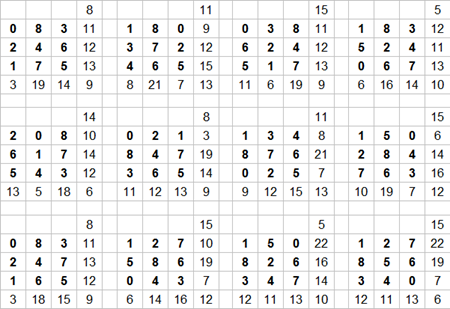
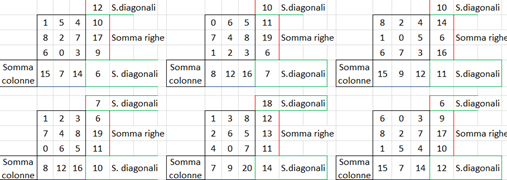
I solutori per la classe seconda, con le rispettive soluzioni, sono stati:
Antonella:
Dopo la prima soluzione le altre le ho ottenute scambiando
l'ordine dei numeri. Ecco i risultati
Gian Franco:
Ho trovato prima quattro soluzioni per tentativi, poi ho trovato le altre cercando di invertire i numeri senza cambiare le somme, per esempio ho invertito i numeri della prima riga con quelli dell'ultima e ho fatto la stessa cosa con le colonne.
Alessia:
-Mi pare mi abbia detto di aver trovato tutte le soluzioni per tentativi, Ma aiutata molto dalle formule di Calc. E’ così Alessia?
Erika
-Erika, purtroppo solo tre erano le soluzioni corrette:
Giuseppe
- Giu’, ho trovato due soluzioni non esatte: divieto!
Miriam:
per trovare la prima soluzione ho fatto tantissimi tentativi.. poi per le altre ho seguito delle ''regole'':
ho invertito le righe e le colonne dei numeri.
Per trovare la seconda soluzione ho invertito le colonne laterali (della prima soluzione)
per la terza soluzione ho invertito le righe superiore e inferiore(della seconda soluzione)
per trovare la quarta soluzione ho invertito le colonne laterali (della terza soluzione)
e cosi via .. con questo metodo sono riuscita a trovare le 18 soluzioni.
Infine, Antonio, ci ha provato e ha inviato l’immagine del suo quaderno, per altro non troppo ordinata, che conteneva però diversi errori. Io penso che la prossima volta ci proverà con più convinzione. Dico bene, Antonio?
I solutori per la classe terza:
Gabriele G.
le spiego come ho ragionato:
per le prime sette soluzioni stavo ancora provando per tentativi, ma poi mi sono "stufato" [era ora!] e ho cercato un metodo semplice e veloce che mi permetta di trovare dei quadrati con le somme dei numeri tutte differenti, cioè:
[...] ho spostato la prima colonna facendola diventare prima riga, idem con la prima riga e poi [...]
spero di essere stato chiaro :)
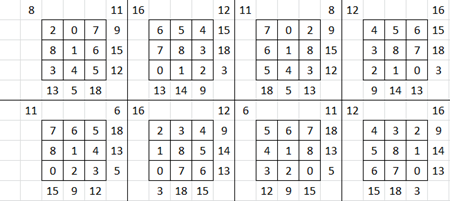
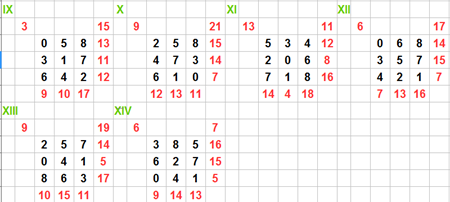
No, non lo sei stato, infatti: omissis! Ecco le tue soluzioni
Manuel:
Marco:
Pierluigi, Bachisio e Pietro P. mi consegnano foglietti, dunque:
Pierluigi: 7 soluzioni; Bachisio: 10 soluzioni, Pietro: 2 soluzioni.
Quesito n° 2, sommare le aree di tutti i triangoli in figura

Qualcuno ha lavorato bene fin dal primo tentativo, qualcun altro ha necessitato di invito alla ricerca di altri triangoli.
Per la seconda hanno trovato la soluzione corretta:
Alessia, Elisa, Arianna, Gian Franco, Antonella, Miriam, Giuseppe P. e Erika
Al solito copio incollo sintetizzando, dai loro scritti:
Nella figura ci sono 6 triangoli.
I più piccoli sono AVB, BVC e CVD.Tutti questi hanno base 1 cm e altezza 2 cm, perciò hanno area 1 cm^2.
Poi ci sono i triangoli AVC e BVD. Entrambi con base 2 cm e altezza 2 cm. Perciò area 2 cm^2.
L'ultimo ''triangolone'' è AVD. Con base 3 cm e altezza 2 cm, perciò area 3 cm^2
Sommando tutte le aree (1+1+1+2+2+3) ottengo un’area di 10 cm^2.
Qualcuno ha fatto anche la costruzione su GeoGebra.
Copio le immagini di quella di Gian Franco che ha voluto integrare la soluzione. Si è presa una certa licenza, io l’ho concessa con qualche dubbio...
I triangoli in figura sono 6:
se si uniscono tutti questi triangoli si forma un rettangolo:
Posso formare questa figura perché il triangolo verde ha la stessa base e altezza di quello rosso quindi anche la stessa area, quindi per completare il rettangolo ho trasformato quello verde in quello rosso (del rettangolo)
Il rettangolo ha la base di 5 cm e altezza di 2 cm perciò l' area totale è di 10 cm^2
Antonio ha inviato la soluzione (per l’esattezza più tentativi di soluzione) anche di questo quesito. Non so se devo accettare l’ultima, considerando una svista il suo dato finale: 11 cm^2 anziché 10 cm^2 – Trova i 6 triangoli ma... ? -
Per la terza hanno dato la soluzione:
Bachisio, Gabriele G., Marco, Manuel, Pierluigi, Pietro P., Davide A.1.
Quasi tutti inviano la soluzione su GeoGebra, con le stesse considerazioni della soluzione precedentemente esposta.
Mi pare proprio di aver concluso. Come sempre, segnalatemi eventuali dimenticanze o sviste.
E, come sempre, BRAVO a chi ha lavorato. A prescindere dai risultati ottenuti.
Grazie al prof Davide e
l’appuntamento domani pomeriggio qui per i nuovi quesiti
Etichette: matematica ricreativa, Sarà mica matematica
giovedì 13 novembre 2014
Sarà mica matematica 31
Uuh! a momenti scordavo di segnalare il
Sarà mica matematica 31
del simpaticissimo prof Davide
- Sono appena giustificata, solo un po’ però, torno ora da ennesima riunione ...
Va bene che alcuni di voi hanno già visto tutto e già trovato qualche soluzione. Per i più distratti invece...
Dunque: quesiti divertenti, non complessi, scoperte di strani quadrati [quadrati icigam, booh, non sono proprio riuscita a trovarli in nessun dove! Tranne che, naturalmente, dove si trovano i tesori ...]
Questo invece lo conoscevo
Per scoprire anche voi quelli strani, cliccate sulla figura!
E scoprire ovviamente entrambi i quesiti.
Raccomandazione: leggere con attenzione le richieste, soprattutto quella del quesito n° 2!
Buon divertimento,
grazie, prof Davide.
Etichette: matematica ricreativa, Sarà mica matematica
martedì 11 novembre 2014
Due a settimana..._8, le soluzioni
Arrivano, arrivano...
le soluzioni del Due a settimana..._8
La semplicità dei quesiti ha incoraggiato, almeno in parte, qualche solutore in più della seconda. E’ arrivata invece qualche soluzione in meno da parte della terza: forse troppo facili?? Mah!
Eccole, le soluzioni:
Quesito n° 1, il numero mancante
Per la classe seconda, hanno risposto: Antonella, Alessia, Miriam, Elisa e Arianna, Gian Franco, Daniele, Giuseppe P., Mattia, Daniel, Michele, Cristiana, Erika.
Per la classe terza: Gabriele G., Pierluigi, Manuel, Pietro P., Pietro S., Bachisio.
Tutti hanno facilmente trovato la regolarità nella tabella (come al solito, copio-incollo le spiegazioni più chiare, espresse in buon italiano):
- I numeri delle colonne sono multipli in successione:
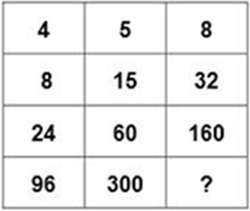
nella prima colonna il primo numero viene moltiplicato per 2, il risultato per 3, il nuovo risultato per 4.
Nella seconda colonna il primo numero viene moltiplicato per 3, il risultato per 4, il nuovo risultato per 5
Nella terza colonna il primo numero viene moltiplicato per 4, il risultato per 5, e per logica il nuovo risultato dovrebbe essere moltiplicato per 6.
Si deduce, quindi, che il numero mancante è 960.
Mi piace quel che scrive Gian Franco:
Il numero che manca nella tabella è 960: l'ho trovato pensando un po' alle successioni che ci proponeva a scuola l'anno scorso, infatti i numeri della tabella, in verticale, sono proprio successioni. [tabella] Il ragionamento è che si moltiplica sempre per numeri successivi, nel primo caso si inizia per 2, nel secondo per 3 e nel terzo per 4.
Questa la tabella presentata da quasi tutti:
Quesito n° 2, spiegare la tovaglia
Per la classe seconda, hanno risposto: Antonella, Alessia, Miriam, Elisa e Arianna, Gian Franco, Giuseppe P., Cristiana, Erika.
Per la classe terza: Gabriele G., Pierluigi, Manuel, Pietro P., Pietro S., Davide A.1, Bachisio.
I ragionamenti:
- Il perimetro della tovaglia, completamente aperta, è uguale a: (24 cm x 4) x 4 = 384 cm: perché il lato della tovaglia (l) viene piegato 4 volte (quindi 24 cm = 1/4 di l) e quindi per sapere la sua misura basta moltiplicare la lunghezza del quadrato piegato (24) per 4 e questa a sua volta deve essere rimoltiplicata per 4 per ottenere il perimetro = 384 cm.
- Il quadrato piccolo ha il lato di 24 cm quindi, siccome il lato del quadrato grande contiene 4 lati del quadrato piccolo, faccio 24 cm x 4=96 cm. Quest'ultimo (che è il lato del quadrato grande) lo moltiplico a sua volta per 4 per trovare la somma dei 4 lati cioè il perimetro che è 384 cm.
- Ho eseguito passo passo le istruzioni del quesito su un foglio di carta, arrivando al quadrato con lato 24 cm. Da lì in poi ho iniziato ad ''aprire la mia tovaglia''. La prima apertura (che trasforma il quadrato in rettangolo) mi porta a un lato doppio [a una dimensione del rettangolo] di 48 cm (24 x 2), continuando ad aprire arrivo ad un quadrato (che ha sempre lato 48), aprendo ancora ottengo un altro rettangolo, la misura di un lato raddoppia, è perciò 96. Aprendo per l'ultima volta ottengo un quadrato di lato 96 e quindi devo moltiplicare 4 (per trovare il perimetro): 96 cm (lato tovaglia aperta) x 4=384 cm: perimetro tovaglia aperta.
- Ho “piegato la tovaglia”: ottengo 2 rettangoli, poi 4 quadrati, poi 8 rettangoli e i rettangoli in due e ho in tutto 16 quadrati. Siccome ogni quadrato ha lato 24 cm ho fatto 24 per 16 e mi da 384 cm ed è il perimetro della tovaglia.
Molti hanno fatto la costruzione su Geogebra (bene!),
altri hanno inviato le foto dell’operazione (più o meno sfocate ma, altrettanto bene!)
Ok, se ho scordato qualcuno mi avvertirete, BRAVO a chi ha lavorato.
Ora (non so se riesco prima di rientrare a scuola) vado a leggere le soluzioni dal prof Davide, non l’ho ancora fatto. Siete pregati di leggerle anche voi. Anzi, facciamo così, è un compito: mi dovrete informare voi sulle risposte dei vostri coetanei della Lombardia!
Etichette: Due a settimana, matematica ricreativa
venerdì 24 ottobre 2014
Due a settimana..._8
Cari ragazzi,
voi di casa e del prof Davide,
vi chiedo scusa per il ritardo ma i nuovi giochi arrivano!
Credo abbastanza semplici, consideriamoci ancora in fase di allenamento.
Quesito n° 1, aritmetico
Nella tabella che vedete in figura manca un numero. Osservatela con attenzione:
Qual è il numero che completa la tabella?
Spiegate il ragionamento seguito per trovare il numero da sostituire al punto di domanda.
Quesito n° 2, geometrico
Una tovaglia quadrata dopo essere stata stirata viene piegata: una prima volta per formare due rettangoli sovrapposti e una volta per formare un quadrato più piccolo.
Una terza e quarta piegatura ripetono, con le stesse modalità, le due piegature precedenti.
Alla fine di queste operazioni, la tovaglia è ridotta a un quadrato di 24 cm di lato.
Qual è la misura del perimetro della tovaglia, completamente aperta, espressa in cm?
Ovviamente, motivate la risposta.
Buon divertimento a tutti.
La scadenza: domenica 9 novembre ‘14. Notate i due giorni in più: per farmi perdonare il ritardo
Etichette: Due a settimana, matematica ricreativa
lunedì 20 ottobre 2014
Sarà mica matematica 30, le nostre soluzioni
Si è ricominciato
e siamo alle soluzioni del primo
Sarà mica matematica del prof Davide, di quest’anno scolastico, che è precisamente il numero 30.
Quesito n° 1, ricostruzione di un'espressione, contenente solo le operazioni di addizione e sottrazione e le giuste parentesi, da una sequenza di numeri
Di seguito i solutori per la classe seconda, con le rispettive soluzioni:
Alessia: (18+12)+(18-16-1)-4-(23-7+11)=0
Gian Franco: [18+12+18-(16+1)-4-23+7]-11 =0
Miriam: [18+12+18-(16+1)]-4-23+7-11=0
Antonella (new entry nella nostra classe, benvenuta nei giochi!): 18+(12+18-16)-1-4-23+7-11 = 0
Elisa e Arianna: 18 + (12 + 18) - (16 + 1 + 4) - 23 + 7 - 11 =0
Cristiana: (18-12)+18-(16-1)-4-(23-7-11)= 0
Antonio: (18+12) +18-16-1-4-23+7-11=0 e (18+12+18-16)-(1+4)-23+7-11=0
Giuseppe P. : 18+12+18-(16+1+4+23-7+11) = 0
Solutori e soluzioni per la classe terza:
Gabriele: (18+12+18)-(16+1+4+23)+7-11=0
Pierluigi: 18+12+(18-16)-1-(4+23)+7-11=0
Pietro S.: 18+12+(18-16)-(1+4+23)+7-11=0
Marco: (18+12)+(18-16-1)-(4+23-7)-11=0
Bachisio: (18+12+18-16)-(1+4)-[(23-7)+11]=0
Da parte di tutti, penso si potesse fare di più. Si accetta la buona volontà!
Quesito n° 2, geometrico, si chiedeva l'area del parallelogramma in figura. Il quadrato ha lato 1 cm:

Per la seconda hanno risolto:
Alessia: dice di esserle venuto in mente il quesito dei terreni dell’anno scorso e così scrive:
Il triangolo BCD è la metà del quadrato. Se muovo il punto C lungo il lato EF, fino ad arrivare a E oppure a F, l’area del triangolo BCD non cambia perché non cambiano la base e l’altezza. L’altezza non cambia perché EF è parallelo a BD. Il parallelogramma risulta diviso in due triangoli congruenti e quindi la sua area è doppia di quella del triangolo BCD e perciò è uguale a 1 cm^2, come quella del quadrato.
GianFranco:
inizialmente, dopo aver guardato per bene la figura, ho tracciato la retta parallela al lato DF del parallelogramma. Successivamente ho osservato che il triangolo BCD è suddiviso in due altri triangoli disuguali. La parte a sinistra della parallela è uguale al triangolo BEC e la parte destra uguale al triangolo DFC. Il parallelogramma è quindi formato da quattro parti a due a due uguali, che corrispondono a due triangoli BCD. Da tutto questo ho capito che il parallelogramma ha l’area uguale a quella del quadrato. Infine ho calcolato l'area del quadrato cioè: 1 cm*1 cm=1 cm quadro.
Qui sotto la figura realizzata da Gian Franco con geogebra.
Nella costruzione è animato anche il punto C, secondo l’interpretazione di Alessia, trovata poi anche da Gian Franco, in seguito alla mia sollecitazione per la ricerca di una seconda soluzione (che però voleva essere ancora diversa!):
Devo precisare che anche Alessia ha realizzato la costruzione animata su geogebra.
Miriam:
Miriam costruisce su carta e ritaglia. Bello! Ecco le immagini del suo lavoro e il commento:
L'area del parallelogramma è pari a 1 cm^2. Ed è equivalente all'area del quadrato.
Ci sono arrivata osservando la figura e mi sono accorta che due dei tre triangoli che formano il parallelogramma (quelli esterni al quadrato), traslati [cioè trasportati con il movimento di traslazione, ho chiesto io a Miriam di specificare il tipo di movimento rigido nel piano, li abbiamo solo accennati in prima], (il primo, il più grande, viene traslato verso il basso. Il secondo, quello più piccolo, viene traslato verso sinistra), si posizionano nella metà del quadrato non occupata dal triangolo più grande del parallelogramma. Perciò se le due figure si equivalgono l'area del parallelogramma è uguale a quella del quadrato.
area quadrato= 1x1 (lxl)=1 cm^2; area parallelogramma= 1 cm^2
Elisa e Arianna e poi anche Cristiana e Antonella:
La costruzione della figura con Geogebra, data la dinamicità del programma, ha dato davvero una bella mano, e di questo non posso che essere contenta!
Scrivono tutte più o meno così:
ci siamo accorte che muovendo il punto E del parallelogramma fino a farlo coincidere con il punto C, il parallelogramma risulta diviso in due triangoli rettangoli che sono uguali alle due parti del quadrato, quindi se l'area del quadrato è di 1 cm^2 anche quella del parallelogramma è 1 cm^2
Antonio:
conciso scrive (io copio incollo):
l'area del quadrato si ottiene facendo lato per lato, il lato misura cm 1 e quindi l'area è 1 cm^2.
Il quadrato diviso dalla diagonale forma due triangoli uguali. Sappiamo che l'area del parallelogramma si ottiene facendo base per altezza e sappiamo anche che il parallelogramma ha la stessa base e la stessa altezza del triangolo per cui la sua area è 1 cm^2.
E questa è la soluzione a cui io volevo portare Gian Franco...
Anche Giuseppe P., con l'aiuto del babbo, fa lo stesso ragionamento di Antonio: l’altezza del triangolo BCD rispetto all’ipotenusa è anche l’altezza del parallelogramma. L’area del parallelogramma si ottiene moltiplicando la base per l’altezza, che in questo caso corrispondono rispettivamente all’ipotenusa del triangolo e all’altezza relativa all’ipotenusa.
Per la terza rispondono:
Gabriele G. con due soluzioni. Costruisce e spiega su Geogebra. La prima è uguale a quella di Gian Franco:
La seconda è come quella di Miriam:
Si notano i due vettori delle traslazioni.
Pietro S. segue il ragionamento di Antonio e Giuseppe P.:
... la base del parallelogramma è l’ipotenusa del triangolo BCD
la sua altezza è uguale a quella del triangolo [relativa all’ipotenusa]. L’area di un triangolo è equivalente
alla metà di quella di un rettangolo avente stessa base e stessa altezza, il parallelogramma è equivalente al rettangolo di uguale base e altezza e quindi il parallelogramma della figura ha l’area di 1 cm^2.
Manuel, Bachisio, Pierluigi, Davide A.1 e Marco, da buoni terzini, ragionano con formule.
La diagonale del quadrato corrisponde alla base del parallelogramma e quindi =√2
l’altezza del parallelogramma è la metà della diagonale e quindi=√2/2
l’area del parallelogramma è perciò: √2*√2/2 = 1
solo Manuel, Bachisio e, arriva appena in tempo utile la risposta di Davide, si rivelano però veri buoni terzini poiché spiegano perché il risultato di quella formula sia 1:
√2*√2 sarebbe (√2)² e, essendo la radice quadrata l'inversa dell’elevamento a potenza 2, semplificando, il risultato è 2. Quindi 2/2=1.
Bene, mi pare di aver detto tutto, se ho scordato qualcosa o qualcuno, mi si farà notare.
Non mi restano che i complimenti a tutti i solutori, e il grazie al prof. Davide.
Domani tutti qui per i nuovi giochi!
PS: non ho ancora dato il “Pubblica” e così ho potuto leggere la e mail di Marco sulla spiegazione del calcolo con le radici. Che fortuna, Marco! E ora, Pubblica!
Etichette: matematica ricreativa, Sarà mica matematica
lunedì 6 ottobre 2014
Sarà mica matematica 30
Ragazzi,
c’è!
Dal prof. Davide, il
Due quesiti freschi freschi per ricominciare!
Fate clic sull’immagine del quesito geometrico:
Buon divertimento!
- leggete bene quanto dice il prof Davide. Non pensate a “cose strane”...
Etichette: matematica ricreativa, Sarà mica matematica
lunedì 11 agosto 2014
Bella geometria!
Ragazzi,
mi rivolgo a entrambe le classi, anche se in ex-seconda abbiamo già trattato l’argomento.
Parlo di un’attività sugli angoli esterni (ma non solo) dei poligoni.
Se cominciate a guardare il lavoro realizzato da Maestra Renata, mi darete ragione: è bella geometria!
Secondo me vi viene voglia di vederlo tutto e rispondere alle domande. Ché come al solito, maestra Renata vi gratifica!
Cliccate sull’immagine:
Prendeteci gusto!
E’ vero che anche noi sul blog abbiamo diversi lavori sugli
In seconda avevamo provato a vedere questo, ma in classe non funzionava l’applet. Ora dovrebbe essere a posto, c’è un secondo link se dovessero esserci problemi con il primo.
Ma ora, ancora in vacanza, invito voi ragazzi a prendere visione solo dell’applet di Maestra Renata
Grazie, Maestra Renata!
Etichette: angoli esterni di un poligono, geogebra, Maestra Renata