Carina l’immagine sotto, vero?
Com’è stata creata?
Cliccateci sopra, è spiegato tutto ...
Home page * GeoGebra * Excel * Matematica nella Storia. I Grandi Matematici * Matematica ricreativa * Libri * Le Curve Celebri * Immagini per la Matematica * Tutoriali * Le Formule più belle * Matematica e ... *
Altri modi per visualizzare il blog
INFORMATIVA SULLA PRIVACY E SUI COOKIE
*MATERIALE DIDATTICO *Risorse didattiche e SCUOLA *BLOG DIDATTICI e colleghicheleggo *Risorse EXCEL - OFFICE *Info CREARE e ARRICCHIRE IL PROPRIO BLOG *Altro Blogroll *Condivisioni *Visualizzazione formule matematiche
Carina l’immagine sotto, vero?
Com’è stata creata?
Cliccateci sopra, è spiegato tutto ...
Etichette: Curiosità con Excel, Excel
On line o su carta o maneggiando ... bottoni!
1. Sette triangoli per un esagono
Accostando nel modo corretto i 7 triangoli dati, è possibile ottenere un esagono regolare. Sai dire come?
Clicca sull’immagine per giocare sul foglio geogebra
2. I bottoni
Marta ha 10 bottoni e vuole disporli su un foglio in modo da poter disegnare 5 segmenti consecutivi, tali che su ognuno si vengano a trovare 4 bottoni.
Sei in grado di aiutarla?
Clic se vuoi lavorare su geogebra. Potrà aiutarti la griglia e, volendo, potrai tracciare dapprima i segmenti. ... consecutivi e possono intersecarsi! :-)
Etichette: geogebra, Giochi, giochi geometrici
Segnalo in questo post il lavoro di un amico, che si è divertito a integrare Excel con Google Chart API. Forse il contrario però, Chart API con Excel!
Molti lettori conosceranno Google Chart API.
E’ uno strumento di Google che permette di generare diversi tipi di grafici, in formato immagine, mappe, diagrammi di Venn o anche formule matematiche da incorporare in una pagina web.
Alcuni tipi di grafici sono davvero fantasiosi, non sempre di facile realizzazione mediante gli strumenti dedicati.
Qualche immagine dalla galleria
La pagina di Google code contiene tutte le indicazioni, guida introduttiva, creazione guidata ecc. Il tutto, purtroppo (!) ... non in italiano! :-)
Roberto, utilizza Excel per la base dati dei grafici. Si immagini di avere una tabella con 100, 1000 righe. Basta una formula da trascinare – copiare – e si dispone di un mezzo per visualizzare quando si vuole 100 grafici ...
E inoltre si ha un altro vantaggio: il peso dei grafici è minimo. Se ad esempio si vogliono inviare, esporre dei dati, è sufficiente un link, nessun allegato.
E ancora, Roberto si propone di sviluppare uno strumento che permetta da un grafico excel già fatto, di restituirne il clone fatto con Google Chart API: basta creare al volo un link e inviare quello al posto del file intero!
Ma ecco il lavoro di Roberto: Google Chart API ed Excel
e anche
Se doveste avere necessità di chiarimenti, lasciate qui un commento: ci rivolgeremo a Rob! :-)
Grazie Roberto!
Etichette: Excel, Google Chart API, Segnalazioni
diventare campioni. Sempre! :-)
Ragazzi,
Due esercizi interessanti. Dovrete ripassare le proprietà ... opportune! (rette e angoli ...).
1. Osserva la figura. L’ampiezza dell’angolo α è sette volte β
Quanto misura α?
2. Più impegnativo. Solo un poco ...! (se no, che campioni sarete?)
Osserva la figura. L’angolo α supera di 10° il triplo di β.
Quanto misura γ?
Ragazzi,
ma si, per diventare campioni :-) Provate!
1. Papà Quasimodo possiede un podere della forma disegnata sotto. Quattro bellissime querce sono piantate in questo podere. Quasimodo decide di dividere il suo podere per i suoi quattro figli in quattro porzioni della stessa forma in modo che ogni porzione contenga una quercia.
Aiuta Quasimodo a fare la ripartizione, disegnando sulla mappa il confine delle quattro porzioni (copiate o stampate l’immagine).
(Campionati internazionali di Giochi Matematici)
2. Quanti triangoli si possono vedere nella figura?
Etichette: Giochi, giochi geometrici, matematica ricreativa
Ragazzi,
curiosa storiella. Anzi due storielle, per la precisione!
Alla fine di una delle prime primavere dell’inizio del XVIII secolo, il matematico svizzero Jean Bernoulli contemplava, dalla sommità di una piccola duna, lo spettacolo delle onde che si infrangevano su una lunga spiaggia dell’oceano Atlantico.
Fu distratto dall’abbaiare di un cane che correva dietro il suo padrone. Quest’ultimo avanzava con una falcata regolare, sempre alla stessa velocità e nella medesima direzione. Il cane, un po' a sinistra del suo padrone, modificava sempre la sua traiettoria in modo che ciascuno dei suoi passi lo dirigesse verso l’estremità dell’ultimo passo del suo padrone.
Evidentemente, poiché il cane corre più veloce del padrone, lo raggiungerà prima o poi. Ma, se supponiamo che la velocità del cane sia la stessa del padrone, la traiettoria del cane risulta molto più interessante.
Si tratta della traiettoria che Bernoulli studiò sotto il nome di curva del cane.
Interessante il comportamento della curva dopo un certo tempo sufficientemente grande: si constata che il cane si avvicina sempre più alla retta M seguita dal padrone.
Si può anche constatare che il cane si avvicina sempre più al suo padrone.
Col passare del tempo l’animale è praticamente “sulla” traiettoria del padrone, a una certa distanza dietro di lui. Si intuisce che questa distanza tra il cane e il padrone diminuisce progressivamente tendendo a stabilizzarsi su un certo valore-limite.
Riguardo a questa curva però c’è anche una storiella diversa!
Il medico francese Claude Perrault (visse nel 1600), anatomista e architetto, fratello di Charles Perrault, il creatore di Cenerentola, Cappuccetto Rosso, Il gatto con gli stivali, divenne famoso in campo matematico in quanto un giorno, giocherellando con il suo orologio da taschino, lo piazzò in mezzo al tavolo e cominciò a tirare l’estremità della catena lungo il bordo del tavolo.
E si domandò: qual è la forma della curva che il mio bell’orologio sta descrivendo?
Non riuscendo a venirne a capo, passò la richiesta all’amico Leibniz e ad altri matematici. Leibniz non tardò a riconoscere che la curva cercata è caratterizzata dalla proprietà che per essa è costante il segmento di ogni tangente compreso tra il punto di contatto e l’intersezione con una retta fissa. Per questo la curva viene detta anche equitangenziale.

Huygens, un altro matematico, si occupò a fondo della stessa curva e la chiamò tractoria, dal latino trahere, “tirare”, “trascinare”. Oggi a tractoria si preferisce il nome di trattrice; altri usano il nome di traiettoria di Huygens.
Se al posto dell’orologio immaginiamo di avere un ... cane, al posto della catena un guinzaglio, e il padrone del cane che lo tiri lungo un percorso rettilineo, ritroviamo la curva del cane!
Clic sull’immagine per vedere la passeggiata! Su Geogebra.

Da
Addomesticare l’infinito – A. Deledicq – F. Casiro - Edizioni Kangourou Italia
e
Le Curve Matematiche tra curiosità e divertimento - L. Cresci
Etichette: curva del cane, curve celebri, geogebra, trattrice
Ragazzi,
leggete la seguente situazione e provate a rispondere alla domanda. Dovreste riuscire! E se proprio no, sarà una nostra attività ...
Il Signor Carlo scende dal tram all’incrocio di via Pietro Micca con via Antonio Giuseppe Bertola (nella mappa che vedi qui sotto il punto è contrassegnato da un asterisco)
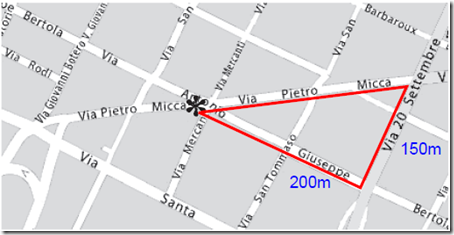
Quanti metri all’incirca percorre al ritorno?
A. Possono essere 200 metri? Motiva la tua risposta. (il solo SI o NO non è valido!)
B. Possono essere meno di 200 metri? Motiva la tua risposta. (come sopra!)
C. Possono essere 350 metri? Come sopra, giustifica la risposta.
D. E ... 600 metri?
Dunque? Dite voi quanti metri all’incirca!
NOTA: qualche adulto potrebbe dirvi che “ci vuole il teorema di Pitagora”. Se ne può fare a meno! Infatti:
1. Non vi chiedo la lunghezza esatta del percorso, ma solo all’incirca.
2. Dovreste essere in grado di rispondere alle domande A, B, C e D, con le conoscenze già in vostro possesso (ehm ... triangoli, distanza in geometria)
Etichette: Problemi geometrici, Triangoli
Ragazzi,
e ora la “sorpresa” fra le spirali equiangolari.
Osservate la figura
Ora non pensate all’angolo, alla suddivisione dell’angolo giro di cui abbiamo parlato finora.
Vi domando invece se la costruzione vi ricorda qualcosa...
Osservate in figura la serie di rettangoli. (La spirale passa però sui vertici di quadrati, voi concentratevi sui rettangoli) Mmh.. vi dice nulla? Pensateci un po’, su!
Ma se proprio avete il “vuoto”, sono certa che visualizzando l’animazione, riconoscerete ... !:-)
Etichette: geogebra, spirale equiangolare, spirali
QUI, nella costruzione della spirale equiangolare, abbiamo visto la decrescita esponenziale, verso l’infinitamente piccolo ...
Viceversa...
Osservate l’immagine sotto.
Ancora dividendo l’angolo giro in 6 parti uguali, in angoli cioè di 60°,
e si costruisce BC ⊥ (perpendicolare) AB;
si ha: AC = 2 AB; (angolo BAC = 60°)
si continua costruendo CD ⊥ AC;
si ha: AD = 4 AB; (angolo BAD = 120°)
e ancora:
DE ⊥ AD; si ha: AE = 8 AB; (angolo BAE= 180°)
e così di seguito.
Si può ben dire: verso l’infinitamente grande!
Si ha in questo caso una progressione geometrica di ragione 2. La progressione geometrica delle potenze di 2, che abbiamo visto nell’esempio.
E ancora, se
in generale x = n° angoli e y = distanza da A,
si ha: y = 2^x
E’ la legge dell’accrescimento esponenziale, rappresentata sul piano cartesiano dal grafico qui sotto
Anche stavolta grafici ben diversi per la stessa legge!
Ora clic per aprire l’applet geogebra.
Possiamo costruire una spirale equiangolare anche partendo da un angolo più piccolo, per esempio da un angolo di 30°, suddividendo cioè l’angolo giro in 12 parti uguali.
Per il momento (riferito a quando ci lavoreremo su!) osservate l’immagine, più avanti potremo comprendere meglio la progressione geometrica che ritroviamo in questa spirale (di ragione (radice quadrata di 3 )/ 2):

Eh, non vi avevo detto che avremmo confrontato diverse spirali?
La spirale equiangolare ha affascinato i più grandi scienziati del 1600: Cartesio (quello del sistema di riferimento cartesiano!), Galileo, Torricelli.
Il matematico svizzero Jakob Bernoulli (1654 – 1705) definì la curva “Spira mirabilis”, la spirale meravigliosa, disponendo che essa fosse scolpita sulla sua tomba, a Basilea, accanto alla frase “Eadem mutata resurgo”, ovvero “sebbene diversa, rinasco identica”. In onore al matematico la curva viene anche chiamata di Bernoulli.
Per quanto riguarda la pietra tombale sfortunatamente lo scultore sbagliò: incise una spirale uniforme, quella di Archimede!
E ... con le spirali equiangolari non è mica finita. Ci sarà pure una sorpresa!
Ah, le ritroviamo spesso in natura!
Guardate anche QUI le immagini ...
Queste attività sono sempre tratte da
Matematica nella Realtà
E. Castelnuovo, M. Barra
Etichette: geogebra, spirale equiangolare, spirali
Ragazzi,
Avevo detto che avremmo confrontato curve spirali diverse.
La spirale di Archimede, ricordate (o ri-vedete), è ottenuta tracciando delle circonferenze in modo continuo, aumentando il raggio in modo proporzionale all'angolo percorso.
Un altro tipo di spirale può ottenersi dividendo l’angolo giro in 6 parti uguali, in angoli cioè di 60°. Osservate l’immagine (più sotto, ci sarà il link per l’applet):
e si costruisce BC ⊥ (perpendicolare) AC;
si ha: AC = 1/2 AB; (angolo BAC = 60°)
si continua costruendo CD ⊥ AD;
si ha: AD = 1/4 AB; (angolo BAD = 120°)
e ancora:
DE ⊥ AE; si ha: AE = 1/8 AB; (angolo BAE= 180°)
e così di seguito.
Si può ben dire: verso l’infinitamente piccolo!
In matematica si dice che si ha una progressione geometrica di ragione 1/2. [Qui sul blog abbiamo visto le progressioni aritmetiche, nelle quali la differenza fra qualsiasi termine ed il suo precedente è costante].
Si dice progressione geometrica (o per quoziente) una successione di numeri in cui è costante il quoziente fra un qualunque numero e il suo precedente.
Quindi, a partire da un termine iniziale (diverso da zero), ogni altro termine si ottiene moltiplicando il precedente sempre per uno stesso numero diverso da zero. Tale numero è detto ragione della progressione.
Es:
- La progressione geometrica delle potenze di 2:
1, 2, 4, 8, 16, 32, 64, 128, 256, 512, … ha termine iniziale 1 e ragione 2.
- La progressione geometrica delle potenze di 3:
1, 3, 9, 27, 81, 243, 729, 2187, 6561, … ha termine iniziale 1 e ragione 3.
- La progressione geometrica delle potenze di 1/2:
1, 1/2, 1/4, 1/8, 1/16, 1/32, 1/64, 1/128, 1/256, ... ha termine iniziale 1 e ragione 1/2.
Quest’ultimo esempio è quello che si presenta nella nostra costruzione della spirale:
la lunghezza dei segmenti, a seconda dell’angolo descritto a partire da AB, in senso antiorario, varia via via in ragione di 1/2.
In generale se x = n° angoli e y = distanza da A,
si ha: y = 1/2^x
E’ la legge della decrescita esponenziale, rappresentata sul piano cartesiano dal grafico:

Ora, per aprire l’applet geogebra, clic qui.
Al prox post: verso l’infinitamente grande...
Etichette: geogebra, spirale equiangolare, spirali
Stavolta da L’uomo che sapeva contare,
due enigmi.
Dei quali però, ragazzi, (e, eventualmente, lettori) lascio a voi il gusto della soluzione!
Enigma n° 1:
La vendita di mele
« ... Le tre ragazze furono condotte dal qadi [un giudice], il quale così parlò: ‘Qui ci sono 90 mele che dovete vendere al mercato. Tu, Fatima, la più grande, ne prenderai 50, e tu, Cunda, 30; mentre tu, Shia, che sei la minore, ne avrai 10. 
Se Fatima vende le sue mele al prezzo di 7 per un dinaro [7 mele ---> 1 dinaro], anche voi due dovrete fare lo stesso. E se invece Fatima le vende a 3 dinari per mela, [1 mela ---> 3 dinari] , allora anche voi le venderete alle stesse condizioni.
Ma, qualunque cosa facciate, ciascuna di voi dovrà alla fine avere incassato la stessa somma di denaro, pur vendendo quantità diverse di mele’.
Le tre sorelle non sapevano proprio come venire a capo del problema, che si presentava assurdo. Dal momento che dovevano vendere le mele allo stesso prezzo, il ricavato di 50 mele sarebbe stato necessariamente di gran lunga superiore a quello di 30 o di 10 mele.
Per chiedere consiglio si recarono da un sant’uomo che viveva nei paraggi. Dopo aver riempito di conteggi alcuni fogli, egli si espresse in questi termini: ‘Ragazze, la soluzione è chiarissima. Vendete le 90 mele proprio come il qadi vi ha ordinato, e tutte e tre otterrete lo stesso profitto.’ Diede poi alle tre sorelle delle istruzioni....
... Le ragazze andarono al mercato e vendettero le mele seguendo le indicazioni ricevute. Cioè Fatima ne vendette 50, Cunda 30 e Shia 10, tutte allo stesso prezzo, e ciascuna delle tre ottenne lo stesso guadagno!
In che modo il sant’uomo poté risolvere il problema?»
Aiut(ino) - per i ragazzi -: le mele possono essere vendute in più fasi.
Enigma n° 2:
« Dal libro di Bhaskara il Sapiente, famoso geometra e astronomo indiano, il Lilavati, che era il nome di sua figlia...
‘La quinta parte di uno sciame d’api si posò sul fiore di Kadamba, un terzo sul fiore di Silinda. Tre volte la differenza tra questi due numeri volò su di un fiore di Krutaja, e solo un’ape rimase in volo, attratta dal profumo di un fiore di gelsomino.
Dimmi, bellissima fanciulla, quante erano le api in quello sciame?»
Aiuto per i ragazzi (che hanno fatto solo la prima media):
visualizzate la situazione con uno schema, per es. con i “segmentini”; ricordate però che dovete prima trasformare le frazioni in altre equivalenti che abbiano uguale denominatore (proprietà ... ?).
Se avviate ma vi bloccate su qualche punto, scrivete pure! :-)
Etichette: Giochi, Libri, matematica ricreativa
Ancora da L’uomo che sapeva contare...
Beremiz, l’Uomo Che Conta, racconta una delle meraviglie dell’aritmetica:
“usando quattro quattro si possono ottenere tutte le cifre del sistema decimale”
andate a vedere il girotondo delle combinazioni sull’applet GeoGebra, per i numeri da 0 a 10, cliccando sull’immagine.
Oppure ... :-)
Etichette: geogebra, Giochi, Giochi matematici, Libri, matematica ricreativa
Relax estivo...
“... «Astir ha 16 anni». E aggiunse, con una punta di sospetto
«Volevo solo dare un piccolo suggerimento»; rispose Beremiz. «Se tu eliminassi dalla mandria l’animale difettoso, il totale sarebbe di 256, che è il quadrato di 16; cioè 16 volte 16. Il dono offerto al padre della deliziosa Astir avrebbe allora una certa perfezione matematica, essendo il numero dei cammelli uguale al quadrato dell’età dell’amata. Il numero 256 è esattamente una potenza del 2 — nell'antichità vi si annetteva un valore simbolico — mentre 257 è un numero primo. Queste relazioni tra quadrati sono di buon augurio per gli innamorati. C’è in proposito un’interessante leggenda. La vorresti sentire? »
« Con molto piacere» rispose il Visir. «Mi piace sempre ascoltare una bella storia, soprattutto se raccontata bene»
Lusingato, L’Uomo Che Contava si inchinò graziosamente e cominciò: « Si narra che re Salomone, dando prova di sapienza e cortesia, donò alla sua fidanzata, la bellissima Belkis, regina di Saba, uno scrigno con 529 perle. Come mai 529? Perché 529 è il quadrato di 23 — cioè 23 volte 23 fa 529 — e la Regina aveva 23 anni. Ma nel caso della giovane Astir, 256 ha un vantaggio rispetto a 529 ».
Tutti guardarono sorpresi l'Uomo Che Contava, il quale continuò tranquillamente: « Le cifre del numero 256 sommate insieme fanno 13. Il quadrato di 13 è 169. La somma delle cifre di 169 è 16. Insomma 13 e 16 hanno tra loro una strana relazione, che potremmo chiamare un’amicizia quadratica.

Ritengo di avere così ampiamente giustificata la preferenza che dobbiamo concedere al numero 256, che è ben più interessante del 257».
Da L’uomo che sapeva contare
Malba Tahan
(già presentato su questo blog: ragazzi, andate a leggere l’altro racconto. Se poi vi fate regalare il libro, ancora meglio!)
Etichette: Libri, matematica e..., matematica ricreativa
Eh, dopo lo zufolo...
ancora Archimede!
Eccome no. Uno dei primi matematici a studiare le proprietà delle curve a spirale, Archimede dedica un’intera sua opera, Sulle spirali, alla curva che prenderà il suo nome.
Per cominciare, ragazzi, andate a guardare quest’animazione. Clic sull’immagine


dopo 1/16 di giro lo spago è di 1 cm;
dopo 2/16 di giro lo spago è di 2 cm;
dopo 3/16 di giro lo spago è di 3 cm; ecc...
La spirale è uniforme, cioè cresce uniformemente, ossia il “passo” è sempre lo stesso.
Guardate l’immagine sotto, realizzata con GeoGebra.
Vedete l’angolo giro suddiviso in 16 parti;
all’angolo pari a 1/16 di angolo giro, corrisponde una circonferenza di raggio 1;
all’angolo pari a 2/16 di angolo giro corrisponde una circonferenza di raggio 2:
e così via.
Si segnano via via i punti di intersezione tra ciascuna circonferenza e la semiretta uscente dal centro A, lato del relativo angolo. Cioè: il primo punto, D, è l’intersezione tra la circonferenza di raggio 1 e la semiretta lato dell’angolo di ampiezza 1/16 di 360°; il secondo punto è l’intersezione tra la circonferenza di raggio 2 e la semiretta lato dell’angolo ampio 2/16 di 360°, e così di seguito.
Unendo successivamente tutti i punti si ottiene la spirale di Archimede (lo spago che si srotola).
Clic sull’immagine per aprire l’applet sulla quale potrete seguire la costruzione

Ogni punto è caratterizzato da due numeri:
D(1; 1/16), E(2; 2/16), F(3; 3/16), ecc....
Se indichiamo con y il numero degli angoli e con x la distanza del punto da A, il raggio dei cerchi, si ha sempre:
y = 1/16 x
Questa è l’equazione della nostra spirale.
Sul piano cartesiano è rappresentata da una retta per l’origine degli assi

Spirale e retta hanno la stessa equazione nei due sistemi di riferimento. Due grafici tanto diversi rappresentano la stessa legge...
Etichette: Archimede, geogebra, spirale di Archimede, spirali
o ...
Come misurare l’area di un cerchio?
Ragazzi, qui abbiamo a che fare ancora con ... l’infinito
Archimede di Siracusa fu il primo a spiegare come calcolare l’area di un cerchio quando si conosca la lunghezza della circonferenza che lo delimita.
_______________________________________________________________
Osservate le immagini: sono le prime due tappe del suo ragionamento.
Spiegazioni e conclusioni nel breve video. Immagini realizzate con Geogebra
L’area del cerchio vale dunque esattamente $π * r^2$
Da
Addomesticare l’infinito – A. Deledicq – F. Casiro - Edizioni Kangourou Italia
Sul testo è riportata anche la traduzione letterale completa del ragionamento di Archimede come si può trovare in greco nell’edizione delle opere di Archimede.
QUI la spiegazione in inglese.
Etichette: Archimede, area del cerchio, circonferenza, geogebra, infinito, matematica nella storia, video

