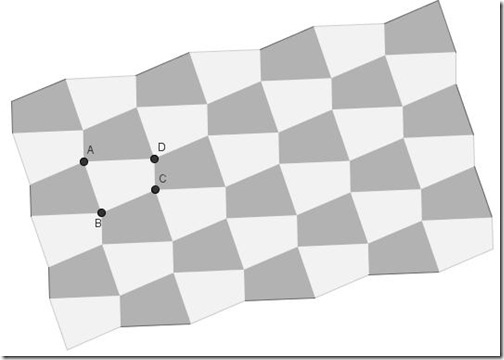
Abbiamo già visto in una nostra attività (e anche qui),
che, fra i poligoni regolari, solo il triangolo equilatero, il quadrato e l’esagono regolare possono tassellare il piano, cioè è possibile “pavimentare” o “piastrellare” il piano accostando i poligoni l'uno all'altro, senza sovrapporli e senza avere degli spazi vuoti tra essi. In ciascuno di tali poligoni l’angolo interno è sottomultiplo di un angolo giro.
E’ però possibile realizzare delle “pavimentazioni” o tassellature, anche con poligoni non regolari.
E’ stato dimostrato che nessun poligono convesso con più di sei lati può tassellare il piano.
Consideriamo dunque i poligoni di tre, quattro, cinque e sei lati.
Tasselli triangolari
Qualunque triangolo può tassellare il piano. Si può costruire il simmetrico del triangolo rispetto al punto medio di uno dei suoi lati: “i lati corrispondenti di due triangoli identici combaciano e si forma un parallelogramma. Com’è ovvio, le repliche di un parallelogramma si possono far combaciare lungo i lati per formare una fila illimitata di lati paralleli, e le strisce, a loro volta, si possono avvicinare l’una all’altra per ricoprire interamente il piano”.
Nella costruzione con geogebra, ho utilizzato solamente successive simmetrie di centro punto medio di un lato dei triangoli. Clic sulla figura per aprire l’applet. Sul foglio di lavoro l’indicazione più semplice se si vuole … estendere la pavimentazione! (ho lasciato visibili solo i segmenti esterni per motivi estetici)
Tasselli a forma di quadrilatero
“Qualunque quadrilatero tassella il piano!” Anche in questo caso si può costruire il simmetrico del quadrilatero rispetto al punto medio di uno dei suoi lati: “i lati corrispondenti di due quadrilateri identici combaciano e si forma un esagono. Ogni lato dell’esagono è necessariamente uguale e parallelo al lato opposto. Tale esagono, con una semplice operazione di traslazione, formerà un motivo tassellante”
Anche in questo caso, con geogebra ho utilizzato successive simmetrie di centro punto medio di un lato dei quadrilateri. Il quadrilatero inoltre può anche non essere convesso. Clic sulla figura per aprire l’applet. Indicazioni sul foglio di lavoro…
Modificando il quadrilatero da convesso a concavo si può avere una figura simile
Tasselli a forma di pentagono
I tasselli a forma di pentagono convesso possono essere classificati in otto tipologie. Cinque furono trovate da Reinhardt. Kershner li descrive contrassegnando i pentagoni per tipi. Nell’immagine il tipo e la tassellatura corrispondente:

Le caratteristiche dei singoli tipi:
|
|
“Non è dimostrato il fatto che non esistano altri pentagoni convessi capaci di tassellare il piano, per l’eccellente ragione che una dimostrazione completa richiederebbe un libro piuttosto voluminoso”
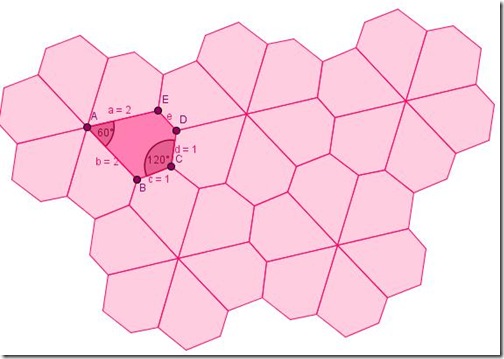
Con geogebra la tassellatura del 5° tipo. Costruita con i passi segg:
- Punto medio del lato e del pentagono ABCDE
- Simmetrico di ABCDE rispetto al punto
- Rotazione di 60° del simmetrico ottenuto, con centro il punto corrispondente del punto A nella simmetria.
- Rotazioni successive di ampiezza 60°, con medesimo centro, dei pentagoni ottenuti.
- Ripetere dal punto 1.
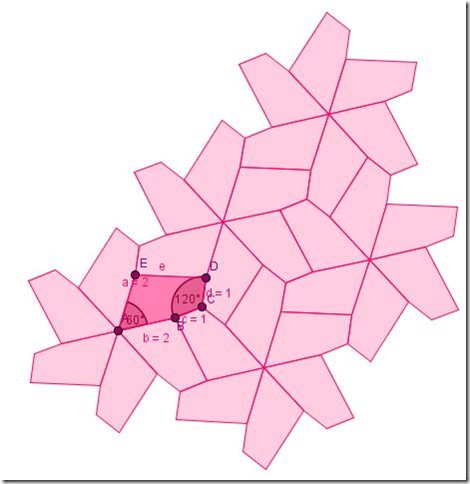
Variando la forma del pentagono, conservando le proprietà di lati e angoli…
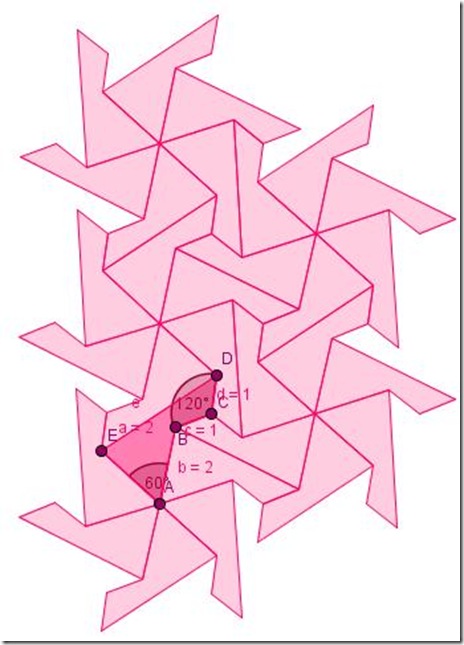
Infine, se il pentagono diventa concavo
Per ora mi fermo qui. In un altro post le tassellature esagonali (almeno) .
Ma quanto altro nel capitolo 13, Mosaici di poligoni convessi, del:
Viaggio nel tempo e altre stranezze matematiche - Martin Gardner – Sfide Matematiche !
- Le scritte in grigio e l’illustrazione dei tipi-tasselli pentagonali, dal testo.-
Link sulle Tassellazioni del piano:
Matematica e dilettanti
Attività di tassellazione con GeoGebra