III,
eheh i ragazzi, senza troppo "averne l'aria", controllano, controllano sul blog ... :-)
In chiusura del post precedente, sulla simmetria centrale, vi ho detto che avremmo imparato a costruire il simmetrico di un punto rispetto a un altro punto, che costituisca il centro di simmetria.
E no, però, non intendo mica mediante lo strumento Simmetrico rispetto a un punto. Troppo semplice! :-)
Lavoriamo con geogebra, ma dobbiamo simulare la costruzione sul quaderno. Dove non abbiamo "simmetrico rispetto a un punto" !
Che ne dite di provarci da soli?
Consiglio di rivedere prima l'intero post su citato.
Aprite il foglio di lavoro (clic sull'immagine).
Avete a disposizione gli strumenti che potreste utilizzare. Non sono infatti quelli strettamente necessari, per lasciarvi una certa libertà nella procedura. Non vi costringo a una sola soluzione. Discuteremo poi le eventuali diverse strade seguite.
Avete a disposizione anche strumenti di controllo. Vi servono cioè per verificare l'esattezza del risultato.
Sul foglio trovate la sintesi delle proprietà della simmetria centrale, le indicazioni necessarie per operare!
Home page * GeoGebra * Excel * Matematica nella Storia. I Grandi Matematici * Matematica ricreativa * Libri * Le Curve Celebri * Immagini per la Matematica * Tutoriali * Le Formule più belle * Matematica e ... *
Altri modi per visualizzare il blog
INFORMATIVA SULLA PRIVACY E SUI COOKIE
*MATERIALE DIDATTICO *Risorse didattiche e SCUOLA *BLOG DIDATTICI e colleghicheleggo *Risorse EXCEL - OFFICE *Info CREARE e ARRICCHIRE IL PROPRIO BLOG *Altro Blogroll *Condivisioni *Visualizzazione formule matematiche
mercoledì 30 settembre 2009
Costruzione del simmetrico di un punto rispetto al centro di simmetria
lunedì 28 settembre 2009
La simmetria centrale
III,
cominciamo dunque ad approfondire il discorso sulla simmetria.
Meglio, sulle simmetrie...
Come accennato QUI, conosciamo un po' la simmetria per aver incontrato in diversi contesti, figure (o tabelle) che ... si guardano allo specchio, qualche esperimento concreto in classe è capitato anche in questi giorni. Il ribaltamento come movimento rigido, appartiene alle isometrie ed è una particolare simmetria.
In questo post non vi faccio lavorare ancora su quella particolare simmetria.
Intendo riprendere la domanda posta sull'ultima attività nel foglio di lavoro geogebra(tornateci!)
Ma ... cominciamo così:
osservate questa bella Rosa di Grandi a 4 petali
[vi guido con l'immagine:

Strumento, clic sul punto A (oggetto da trasformare), clic su C, centro di simmetria]
Nella rosa abbiamo dunque individuato una simmetria.
Propriamente, si tratta della simmetria centrale:
il punto A' è il punto corrispondente nella simmetria centrale di centro C, al punto A
Ora, fate clic sulla rosa e andate a muovere con il mouse il punto A sul petalo.
Osservate, agite e riflettete:
- il punto A', suo simmetrico rispetto al centro, descrive il petalo simmetrico della curva;
- confrontate le distanze AC e A'C. Potete misurare: strumento Distanza o lunghezza, questo lo conoscete! Cosa osservate?
- i punti corrispondenti A e A' sono allineati. Uniteli usando lo strumento Segmento tra due punti.
- Il punto C dunque, rispetto al segmento AA', cosa rappresenta? Dovrete usare un altro strumento per verificare ...
In quest'ultima domanda dovreste riconoscere quella cui accennavo sopra... (ultimo lavoro sulla rotazione)
Rivediamo l'immagine:

- i punti corrispondenti A e A', B e B' .... sono allineati con il centro E;
- EA = EA'
- E è quindi il punto medio dei segmenti di estremi A e A' , B e B', ...
Una domanda: nella rotazione di 180°, quale parte ha il verso della rotazione? Come deve o può essere? Ripetete l'attività! :-)
Per le caratteristiche descritte i punti A e A', ecc..., corrispondenti nella rotazione di 180°, si dicono simmetrici rispetto al punto E (centro di simmetria).
Due punti qualsiasi P e P' si dicono simmetrici rispetto a un punto O (il centro di simmetria) se O è il punto medio del segmento PP'.
Dunque concludiamo che:
ogni rotazione nel piano di ampiezza α=180° attorno a un centro O, è una simmetria centrale, o simmetria di centro O.
Possiamo anche dire che la simmetria centrale coincide con la rotazione di 180° rispetto al centro di simmetria!
Dobbiamo ora imparare a costruire il simmetrico di un punto rispetto a un altro, centro di simmetria. Vedremo poi la simmetria centrale dei poligoni e individueremo le coordinate sul piano cartesiano.
Alla prox!
Etichette: geogebra, isometrie, rotazione, simmetria, simmetria centrale, trasformazioni geometriche
domenica 27 settembre 2009
Simmetrie ...
I e III A,
sì, sì, anche voi di I (leggete in fondo al post....)
prima di indagare sulla simmetria ... ancora simmetrie. Anche fra le immagini ...
Osservate:


Ragazzi, scaricatelo anche voi, da QUESTA PAGINA. Facilissimo da usare, sono certa che sarete molto più bravi di me! Anzi, propongo una gara artistica: saranno pubblicate le immagini più belle!:-)
Etichette: Immagini per la Matematica, kali, simmetria
sabato 26 settembre 2009
La rotazione sul piano cartesiano in Geogebra
III A,
dopo quello della traslazione, eccovi lo studio della rotazione sul piano cartesiano.
Per individuare le coordinate dei vertici di un poligono ruotato di una certa ampiezza rispetto a un altro, dato il centro di rotazione e il verso, sul vostro quaderno dovreste utilizzare riga e squadra e in alcuni casi goniometro (in quali casi?). Con Geogebra invece... osservate come si fa nel seguente filmato. Clic sull'immagine
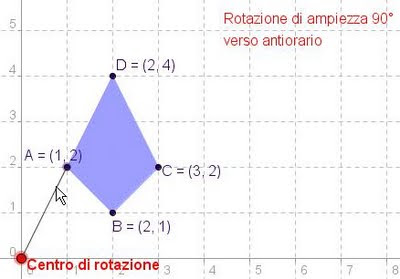
Clic per aprire la finestra del foglio di lavoro:
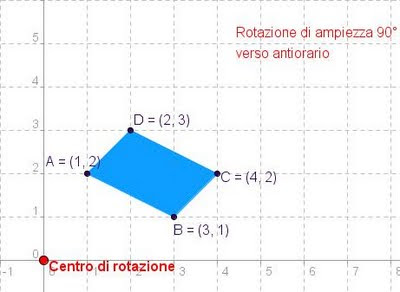
Particolare attenzione va prestata alla rotazione di 180°. Vedi foglio di lavoro.
In proposito ... c'è da sviluppare lo studio delle trasformazioni geometriche! Clic:
giovedì 24 settembre 2009
Esercitazioni con Geogebra sulla traslazione
III A,
come promesso pubblico le esercitazioni guidate da fare on line sul foglio di lavoro dinamico di Geogebra.
1) Come fareste sul vostro quaderno, applicare la traslazione di vettore $\vec{ u }$ assegnato, ad un poligono ABCD e visualizzare le coordinate dei vertici A', B', C', D' . Clic sull'immagine per aprire il video che vi mostra come fare con Geogebra


Si tratta di stabilire (ma è solo una verifica, le coordinate le vedete indicate) la relazione tra le coordinate x e y, dei vertici di un poligono e quelle, x', y', del poligono ad esso corrispondente nella traslazione di vettore dato, tenuto conto delle dimensioni del rettangolo di cui il vettore è la diagonale. Dovete riportare sul vostro quaderno le relazioni trovate dopo ogni modifica del vettore.
(vi ricordo: A(x;y) ----> A'(x ± b_rett; y ± h_rett) così per gli altri vertici; il simbolo ± indica più (+) oppure meno (-), dipende dalla direzione e dal verso del vettore. vero?)
Sul foglio trovate le indicazioni per modificare direzione, verso e intensità (o modulo) del vettore. Clic sulla figura e buon lavoro!
mercoledì 23 settembre 2009
Perché funziona (la carta mancante)
Come promesso nel post "Gioco: calcolo mentale semplice!",
con i ragazzi di I abbiamo discusso sul "perché funziona".
Devo dire che sono stati bravi: qualcuno ha intuito subito che SE nel gioco sommavamo, allora bisognava trovare la somma di tutte le carte ...
Hanno scritto anche le loro relazioni, che insieme abbiamo letto e discusso in classe.
Gabriele scrive la sua al computer e quindi copio-incollo!
Come funziona il gioco della carta mancante
La somma dei valori di tutte le 40 carte è 220 (dopo spiego come si può fare la somma velocemente).
Durante il gioco si toglie una carta, per esempio un 2. Quindi la somma non sarà più 220 ma sarà 218. Nel gioco però si tolgono le decine allora otterremo 8, da 8 bisogna contare quanto manca per arrivare a 10 (o a 0, zero, se tolgo la decina), manca 2 perciò so che è il 2 la carta mancante. Infine si da una sfogliata veloce (durante il gioco) per vedere quale 2 manca (dei 4 semi).
La somma dei valori delle 40 carte.
Provando e riprovando abbiamo trovato un metodo semplice per addizionare i valori di tutte le carte.
Qualche compagno ha detto: "si contano una per una le famiglie" e poi, si conta una famiglia e si moltiplica per 4
Basta contarne solo una e in un modo veloce.
Partiamo da un seme:
anziché fare 1+2+3+4+5+6+7+8+9+10 si può disporre i numeri di 1 seme:
1 2 3 4 5 6 7 8 9 10
poi si mette da parte il 10 , si fa 1+9, 2+8, 3+7, 4+6 = 40 ma voi vi chiederete dov’è il 5 e il10? Adesso lo scoprirete.
Abbiamo 40+5+10 = 50+5 = 55 ma questo è solo uno dei 4 semi.
Per avere la somma di tutti e quattro i semi si fa una moltiplicazione 55*4=220.
Bravo Gabri, bravi tutti! (anche perché (quasi tutti) sapevano e hanno saputo spiegare, che 220 contiene 22 decine! ehmm... non 2, vero? ;-) )
Etichette: calcolo mentale, Giochi, matematica ricreativa
martedì 22 settembre 2009
Per giocare con la rotazione
I ragazzi di III lo sanno che
possono andare a vedere diverse cosette sulla rotazione....
Bisogna però cominciare da QUI!
Ancora per giocare un po', stimolata da maestra Renata - e lei lo sa che mi suggerisce anche delle tecniche...-:), mi sono divertita a creare un balletto di .. lucertoline (?) gemelle!
Boh, ma a voi cosa sembrano?
Sìì, sono lucertole! La coda è così perché le hanno mozzate e stanno ricrescendo doppie! :-)
Béh poche storie, ridete pure, fate clic sull'immagine e divertitevi con la danza! :-))
domenica 20 settembre 2009
Ancora un gioco logico...
Siamo ancora in fase di "accoglienza"...
Dunque ragazzi, il seguente:
Quale figura?
Quale tra le figure A, B, C, D, completa correttamente la serie in basso ?
Fai clic sull'immagine e segui le indicazioni sul foglio di lavoro GeoGebra. (Prima di ricorrere all'aiuto ... rifletti!)
Etichette: geogebra, Giochi, giochi logici, matematica ricreativa
sabato 19 settembre 2009
Un giochino on line!
Ragazzi della prima (ma quanto sono carini!!! E bravi eh! Ci siamo già divertiti con i giochi, bravissimi con il cruci numero e altro ...)
Stavolta ho preparato per voi un giochino da fare on line. Non dovete scaricare niente ma solo fare clic sull'immagine qui sotto. Seguite poi le indicazioni che leggerete sul foglio di lavoro dinamico di GeoGebra (tranquilli, lo useremo insieme... intanto, come abbiamo detto, cominciate a scaricarlo: da QUI).
Dovrete portare in cima al podio uno dei quattro numeri colorati (il 4, il 5, il 3 o il 7?), secondo una logica matematica.
Cercate di spiegare la logica matematica: perché quel dato numero può salire sul podio?
Suggerimento: i numeri posti sui gradini sono legati da simboli delle 4 operazioni. Cioè, eseguite un piccolo calcolo da entrambi i lati con quei numeri e, da entrambi i lati, si arriva a ... il numero giusto!
Etichette: geogebra, Giochi, matematica ricreativa
mercoledì 16 settembre 2009
Palloncini ... ma di accoglienza, no?! :-)
Accoglienza continua...
stavolta lo faccio con i palloncini!!!
I e III naturalmente! B u o n_ a n n o_ s c o l a s t i c o, ragazzi. A voi e le vostre famiglie.
ehmm... che palloncini? ma numerici, ovvio!
Osservate l'immagine, si può ingrandire e stampare oppure (come sempre, meglio, più divertente!) lavorare su un file Excel:
Etichette: Excel, Giochi, matematica ricreativa
martedì 15 settembre 2009
Un cruciverba ... di accoglienza :)
ehi, ragazzi che venite in prima media, ci siamo quasi! (noi si comincia dopodomani 17/09/09) A voi il mio *B E N V E N U T I !*
Attenzione: intendo anche Benvenuti sul blog. Che ora sarà anche il vostro blog. Racconterete anche voi la nostra matematica!
Mi auguro amiate il cruciverba. Ve ne propongo uno numerico.
Potete ingrandire con un clic sull'immagine e stampare, oppure scaricare il file Excel (meglio: avrete un controllo nell'eseguire il gioco!).
Se scaricate il file:
(conoscete Excel, il foglio di calcolo elettronico? Imparerete ad utilizzarlo!)
Per compilare il crucinumeri vi serve solo:
- fare clic su ogni singola cella bianca dello schema (si dice: selezionare la cella ed essa sarà attiva);
- digitare ogni cifra in ogni singola cella;
- premere il tasto Invio.
Sul blog troverete altri cruci e ... imparerete a realizzarli!
Etichette: crucinumeri, Excel, Giochi, matematica ricreativa
domenica 13 settembre 2009
Due curve "di mare"
*Curve di mare*: così titola Luciano Cresci il capitolo 8 de Le Curve matematiche tra curiosità e divertimento.
La prima descritta fra queste curve è la

Il nome concoide deriva dal greco κονκοειδεσ, concheides, e significa simile ad una conchiglia, proprio perché la forma della curva ricorda quella di una conchiglia.
Infatti:

L'equazione della curva in coordinate polari è:
$ρ\,=\, \frac{ a }{ cos(θ)} + c$
l'equazione cartesiana:
$y\, =\,\pm \frac{ x }{ x -a} \sqrt{ c² - (x - a)² }$
Come si costruisce la concoide di Nicomede.
Sia data una retta a, un punto A non sulla retta. Si traccia la retta b perpendicolare ad a e passante per A, con D punto di intersezione con a e con DC di lunghezza fissata c. Si ruota la retta b attorno ad A. Si traccia quindi la circonferenza di centro un punto C1 della retta a e raggio c. Si individuano i punti di intersezione, F e G, della circonferenza con la retta b' (b ruotata di un angolo α).
La concoide è il luogo dei punti F e G.
Clic per visualizzare l'animazione su geogebra, che evidenzia i parametri variabili ...
In particolare si nota che la forma della concoide è sempre simmetrica rispetto alla retta b: questa passa per il polo A e per i vertici della concoide. La retta base a è un asintoto sia per il ramo esterno che per il ramo interno ma la forma del ramo interno della concoide dipende dal rapporto fra i due parametri a e c ossia tra le lunghezze dei segmenti AD e il raggio della circonferenza:
per a ‹ c il ramo interno ha un cappio e il polo è un nodo,
per a = c si una cuspide, il cappio del ramo interno si riduce al polo,
per a › c il ramo interno non passa per il polo e quest'ultimo è un punto isolato della curva.
Per l'animazione "conchiglia" clic QUI
La curva base, anziché una retta, può essere qualsiasi curva.
Se per es. la curva è una circonferenza, e il punto fisso A è un punto della circonferenza, la concoide è una lumaca. Se la lunghezza fissa c è uguale al raggio della circonferenza, la concoide diventa una cardioide
Se la curva base è una spirale di Archimede e il punto fisso è il centro della spirale, la concoide è ancora una spirale di Archimede. (torneremo su lumaca e spirale?)
E ora la seconda curva...
La conchiglia di Dürer
Imparentata con la concoide di Nicomede, la conchiglia di Dürer è una curva studiata dal grande artista, pittore e incisore, e matematico Albrecht Dürer.
Nella sua opera Underweysung der Messung mit dem Zirckel und Richtscheyt descrive un apparecchio per tracciare una curva da lui chiamata Muschellinie (in tedesco, "curva a conchiglia").
La curva ha un ramo di concoide e un altro con andamento sinuoso. Graziosissima nella sua semplicità!
Clic per aprire l'animazione con geogebra.
Etichette: concoide Nicomede, curve celebri, geogebra, Libri, Luciano Cresci, Muschellinie
mercoledì 9 settembre 2009
Il trionfo dello ZERO
Ragazzi,
gustiamoci questa simpatica poesia di Gianni Rodari sulla sorprendente potenza dello Zero, che da valere nulla …. può arrivare a valere eccome!
Il trionfo dello ZERO
C’era una volta
un povero zero
tondo come un O,
tanto buono ma però
contava proprio zero
e nessuno lo voleva in compagnia
per non buttarsi via.
Una volta per caso
trovò il numero Uno
di cattivo umore perché
non riusciva a contare
fino a tre.
Vedendolo così nero
il piccolo zero
si fece coraggio,
sulla sua macchina
gli offerse un passaggio,
e schiacciò l’acceleratore,
fiero assai dell’onore
di avere a bordo
un simile personaggio.
D’un tratto chi si vede
fermo sul marciapiede?
il signor tre che si leva il cappello
e fa un inchino
fino al tombino
e poi, per Giove,
il sette, l’otto, il nove
che fanno lo stesso.
Ma che cosa è successo?
che l’uno e lo zero
seduti vicini,
uno qua l’altro là
formavano un gran dieci:
nientemeno, un’autorità!
Da quel giorno lo zero
fu molto rispettato,
anzi da tutti i numeri
ricercato e corteggiato:
gli cedevano la destra
con zelo e premura,
(di tenerlo a sinistra
avevano paura),
lo invitavano a cena,
gli pagavano il cinema,
per il piccolo zero
fu la felicità.
Lo Zero, usato a volte come sinonimo di Niente, è in realtà un numero speciale che merita un’attenzione particolare.
E’ quella cifra, apparentemente innocua, che nasconde poteri insospettati!
Separa i numeri positivi (+) e quelli negativi (–),
se si trova a destra delle altre cifre ne amplifica il valore (10000… verso l’infinitamente grande),
se sta alla loro sinistra le riduce con altrettanta potenza (0,00001… verso l’infinitamente piccolo).
Pare che il simbolo grafico "O" derivi dalla traccia, lasciata sul terreno, una volta tolto l’oggetto che rappresentava un numero (il numero che non c’è più).
Voi ragazzi della classe prima, conoscete la storia dello zero?
Qui sul blog ne abbiamo parlato. Fate clic sull'immagine per leggere una Storiella.
Etichette: G.Rodari, Matematica e poesia, matematica nella storia
sabato 5 settembre 2009
Il triangolo di Reuleaux
Il triangolo di Reuleaux,
dal nome dell’ingegnere e matematico tedesco Franz Reuleaux (1829-1905) è la più semplice delle curve ad ampiezza costante. La più semplice dopo la circonferenza. La più nota di tali curve infatti è la circonferenza.
E cioè:
un cerchio che rotola su una retta rimane sempre nella porzione di piano compresa tra la retta e
la sua parallela, a distanza uguale al diametro del cerchio.
Si possono costruire altre figure con la stessa proprietà!
Il triangolo di Reuleaux.
Si costruisce partendo da un triangolo equilatero;
si tracciano tre archi di cerchio:
- centro su A, raggio uguale al lato del triangolo, estremi i vertici B e C
- centro su B, raggio come sopra, estremi A e C
- centro su C, raggio ..., estremi A e B
Osserviamo: l’ampiezza di questa figura è uguale alla lunghezza del lato del triangolo equilatero.
Figure più generali dei triangoli di Reauleaux sono i poligoni di Reuleaux; si costruiscono utilizzando un qualsiasi poligono regolare convesso con un numero dispari di lati. Es:
Queste figure sono costituite da un numero dispari di archi di cerchio di ugual raggio (in questo caso la lunghezza delle diagonali del poligono) e possiedono lo stesso numero di vertici, i punti di raccordo tra due archi di cerchio consecutivi.
"Per ottenere figure di ampiezza costanti non è necessario considerare esclusivamente poligoni regolari con un numero dispari di vertici; si può anche utilizzare un poligono irregolare convesso per il quale le lunghezze delle diagonali del poligono che congiungono ciascun vertice coi due vertici opposti sono tutte uguali tra loro. In tal modo dal poligono di partenza si possono tracciare i vari archi di cerchio con raggio uguale alla suddetta diagonale."
clic sull'immagine per ampliamenti...
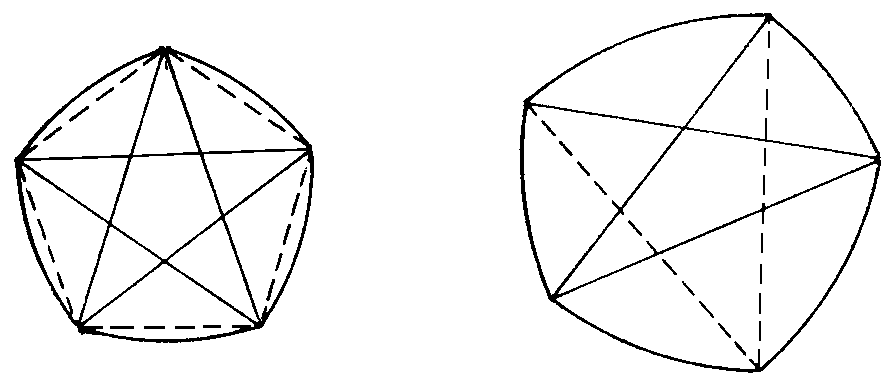
Clic sull'immagine per osservarlo in movimento e verificarne l'ampiezza costante.

Il triangolo di Reuleaux può ruotare in un quadrato, appoggiandosi sui lati con i suoi vertici.
Clic per vedere l'animazione (da geogebra wiki en):
Etichette: geogebra, Triangolo di Reuleaux
mercoledì 2 settembre 2009
Se tu insegni
Riflessioni... di settembre ?
Nell'attesa di rimettermi a lavorare seriamente per il blog, oh, ma pure questa è seria eh?
Se tu insegni ...
Ecco:
ovvero
Se dai del pesce ad un uomo
egli si ciberà una volta.
Ma se tu gli insegni a pescare
egli si nutrirà per tutta la vita.
Se fai progetti per un anno,
semina del grano.
Se i tuoi progetti si estendono
a dieci anni,
pianta un albero.
Se essi abbracciano cento anni,
istruisci il popolo.
Seminando grano una volta,
ti assicuri un raccolto.
Se pianti un albero,
tu farai dieci raccolti.
Istruendo il popolo,
tu raccoglierai cento volte.
Etichette: Poesia e...poesie, riflessioni








































